Binary Search [Lower-bound / Upper-bound]

문제설명

문제

숫자 카드는 정수 하나가 적혀져 있는 카드이다. 상근이는 숫자 카드 N개를 가지고 있다. 정수 M개가 주어졌을 때, 이 수가 적혀있는 숫자 카드를 상근이가 몇 개 가지고 있는지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다. 숫자 카드에 적혀있는 수는 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다.

셋째 줄에는 M(1 ≤ M ≤ 500,000)이 주어진다. 넷째 줄에는 상근이가 몇 개 가지고 있는 숫자 카드인지 구해야 할 M개의 정수가 주어지며, 이 수는 공백으로 구분되어져 있다. 이 수도 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다.

출력

첫째 줄에 입력으로 주어진 M개의 수에 대해서, 각 수가 적힌 숫자 카드를 상근이가 몇 개 가지고 있는지를 공백으로 구분해 출력한다.

접근

[백준] 10815번 숫자 카드 문제와 비슷하면서도 다른 문제이다. 상근이가 같은 숫자가 적힌 카드를 중복으로 가질 수 있고, 그 카드 갯수를 찾는 문제이다. 여기서는 일반 Binary Search가 아닌 Upper Bound와 Lower Bound 알고리즘을 이용해서 중복되는 카드에서 다음과 같이 왼쪽 인덱스와 오른쪽 인덱스+1를 구하고 난 뒤, 찾고자 하는 카드에 대해서 Lower Bound와 Upper Bound의 차를 구하면 카드 갯수를 구할 수 있다.

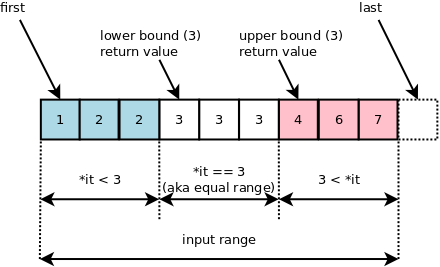
[출처] http://bajamircea.github.io/coding/cpp/2018/08/09/lower-bound.html

[P.S.] Binary Search와 다르게 Lower Bound와 Upper Bound는 right값을 길이보다 1 크게 해야한다. 위 사진에서 7의 Upper Bound를 잘 살펴보자.

코드

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<int> sanggeun;
vector<int> compare;
int n, m;

int lower_bound(int target){
	int left, right, mid;
	left=0, right=n;
	
	while(left < right){
		mid = (left+right)/2;
		
		if(sanggeun[mid] >= target)
			right = mid;
		else
			left = mid+1;
	}
	return right;
}

int upper_bound(int target){
	int left, right, mid;
	left=0, right=n;
	
	while(left < right){
		mid = (left+right)/2;
		
		if(sanggeun[mid] <= target)
			left = mid+1;
		else
			right = mid;
	}
	return right;
}

int main(){
	cin.tie(0);
	cout.tie(0);
    ios_base::sync_with_stdio(false);
	
	int tmp;	
	cin >> n;
	for(int i=0; i<n; i++){
		cin >> tmp;
		sanggeun.push_back(tmp);
	}
	sort(sanggeun.begin(), sanggeun.end());
	
	cin >> m;
	for(int i=0; i<m; i++){
		cin >> tmp;
		compare.push_back(tmp);
	}
	
	for(auto c: compare){
		int u = upper_bound(c);
		int l = lower_bound(c);
		cout << u-l << ' ';
	}
}

참고

[백준] 10815번 숫자 카드
BOJ #10816

이 글이 도움이 되셨다면 추천 클릭을 부탁드립니다 :)