[백준] 1707번 이분 그래프
in Algorithms on BOJ
Graph(BFS/DFS)
문제설명
문제
그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K(2≤K≤5)가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V(1≤V≤20,000)와 간선의 개수 E(1≤E≤200,000)가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호가 빈 칸을 사이에 두고 주어진다.
출력
K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.
접근
이 문제를 풀기위해서는 이분 그래프(Bipartite Graph) 가 무엇인지에 대한 이해가 필요하다.
이분 그래프(Bipartite Graph) 는 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프이다. 즉, 모든 정점을 둘로 분할할 수 있고 서로 다른 그룹의 정점이 연결되어 있는 그래프이다. 아래의 사진 참고.
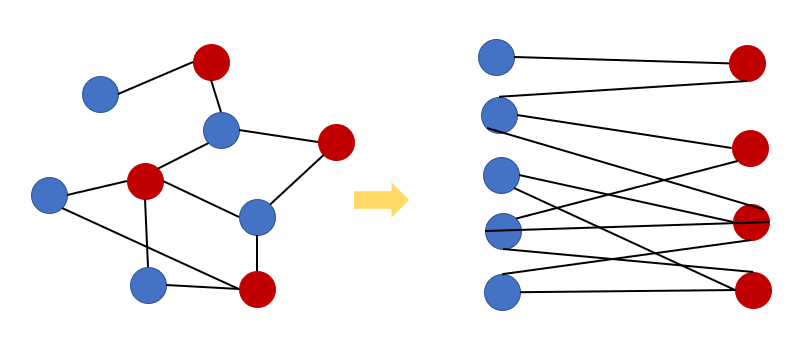 [출처] https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html
[출처] https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html
DFS/BFS 문제를 풀때 사용하는 visited배열을 이용해서 매 정점 방문시 두가지 색상을 표시하면서 이분 그래프(Bipartite Graph) 인지 확인하면 된다. 편의를 위해 BLUE(-1), RED(1), Non-visited(0) 로 표현하였고, 이전 정점 색상에 -1을 곱하면서 인접한 정점을 다른 색으로 표시했다..
주의할 점은 테스트케이스가 2개 이상이기 때문에 visited 배열과 graph 벡터의 초기화를 꼭 해줘야한다.
또 하나 주의할 점은 그래프가 하나의 그래프가 아니고 두개 이상으로 나뉜 그래프가 입력으로 들어올 수 있기 때문에 visited 배열을 사용해서 모든 정점에 대해 확인이 필요하다. 이 조건을 빼먹어서 계속 틀렸다…
코드
#include <iostream>
#include <vector>
#include <queue>
#define MAX_SIZE 20001
#define RED 1
#define BLUE -1
using namespace std;
vector<int> graph[MAX_SIZE];
int visited[MAX_SIZE];
bool isBipartite;
void bfs(int x, int color){
queue<int> q;
q.push(x);
visited[x] = color;
while(!q.empty()){
int current = q.front();
q.pop();
for(int i=0; i<graph[current].size(); i++){
if(visited[graph[current][i]] == 0){
visited[graph[current][i]] = visited[current] * -1;
q.push(graph[current][i]);
}
else if(visited[graph[current][i]] + visited[current] != 0){
isBipartite = false;
return;
}
}
}
}
int main(){
cin.tie(0);
cout.tie(0);
ios_base::sync_with_stdio(false);
int t, v, e;
cin >> t;
while(t--){
cin >> v >> e;
isBipartite = true;
int x, y;
for(int i=0; i<e; i++){
cin >> x >> y;
graph[x].push_back(y);
graph[y].push_back(x);
}
// graph가 2개 이상일 수 있음!!!
for(int i=0; i<MAX_SIZE; i++){
if(visited[i] == 0)
bfs(i, RED);
}
cout << (isBipartite ? "YES" : "NO") << '\n';
// graph, visited 초기화
for(int i=0; i<MAX_SIZE; i++)
graph[i].clear();
fill(visited, visited+MAX_SIZE, 0);
}
return 0;
}
참고
이 글이 도움이 되셨다면 추천 클릭을 부탁드립니다 :)

