[백준] 1967번 트리의 지름
in Algorithms on BOJ
Graph(DFS)
문제설명
문제
트리(tree)는 사이클이 없는 무방향 그래프이다. 트리에서는 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재하게 된다. 트리에서 어떤 두 노드를 선택해서 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우가 있을 것이다. 이럴 때 트리의 모든 노드들은 이 두 노드를 지름의 끝 점으로 하는 원 안에 들어가게 된다.
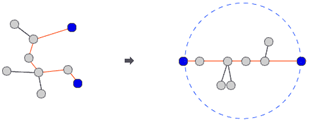
이런 두 노드 사이의 경로의 길이를 트리의 지름이라고 한다. 정확히 정의하자면 트리에 존재하는 모든 경로들 중에서 가장 긴 것의 길이를 말한다.
입력으로 루트가 있는 트리를 가중치가 있는 간선들로 줄 때, 트리의 지름을 구해서 출력하는 프로그램을 작성하시오. 아래와 같은 트리가 주어진다면 트리의 지름은 45가 된다.
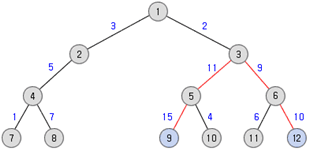
입력
파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n번째 줄까지 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연결하는 두 노드 중 부모 노드의 번호를 나타내고, 두 번째 정수는 자식 노드를, 세 번째 정수는 간선의 가중치를 나타낸다. 간선에 대한 정보는 부모 노드의 번호가 작은 것이 먼저 입력되고, 부모 노드의 번호가 같으면 자식 노드의 번호가 작은 것이 먼저 입력된다. 루트 노드의 번호는 항상 1이라고 가정하며, 간선의 가중치는 100보다 크지 않은 양의 정수이다.
출력
첫째 줄에 트리의 지름을 출력한다.
접근
[백준] 1167번 트리의 지름 문제와 동일한 문제이다. 접근방법은 위의 문제에서 확인할 수 있다. 자세한 설명은 생략한다.
코드
#include <iostream>
#include <vector>
#define MAX_NUM 10001
#define ROOT 1
using namespace std;
bool visited[MAX_NUM];
vector<pair<int,int>> edges[MAX_NUM];
int d[MAX_NUM];
int dfs(int num){
visited[num] = true;
int ret = num;
for(int i=0; i<edges[num].size(); i++){
int nxt = edges[num][i].first;
int cost = edges[num][i].second;
if(visited[nxt] == false){
d[nxt] = d[num] + cost;
int ret_nxt = dfs(nxt);
if(d[ret] < d[ret_nxt]){
ret = ret_nxt;
}
}
}
return ret;
}
int main(){
cin.tie(0);
cout.tie(0);
ios_base::sync_with_stdio(false);
int n;
cin >> n;
for(int i=1; i<n; i++){
int x,y,w;
cin >> x >> y >> w;
edges[x].push_back(make_pair(y, w));
edges[y].push_back(make_pair(x, w));
}
int dv = dfs(ROOT);
fill(visited, visited+MAX_NUM, false);
fill(d, d+MAX_NUM, 0);
int another_dv = dfs(dv);
cout << d[another_dv] << '\n';
}
참고
이 글이 도움이 되셨다면 추천 클릭을 부탁드립니다 :)

