Semantic Segmentation Metric 알아보기
이 글은 Semantic Segmentation Task Metric을 정리한 글 입니다.
Computer Vision Task
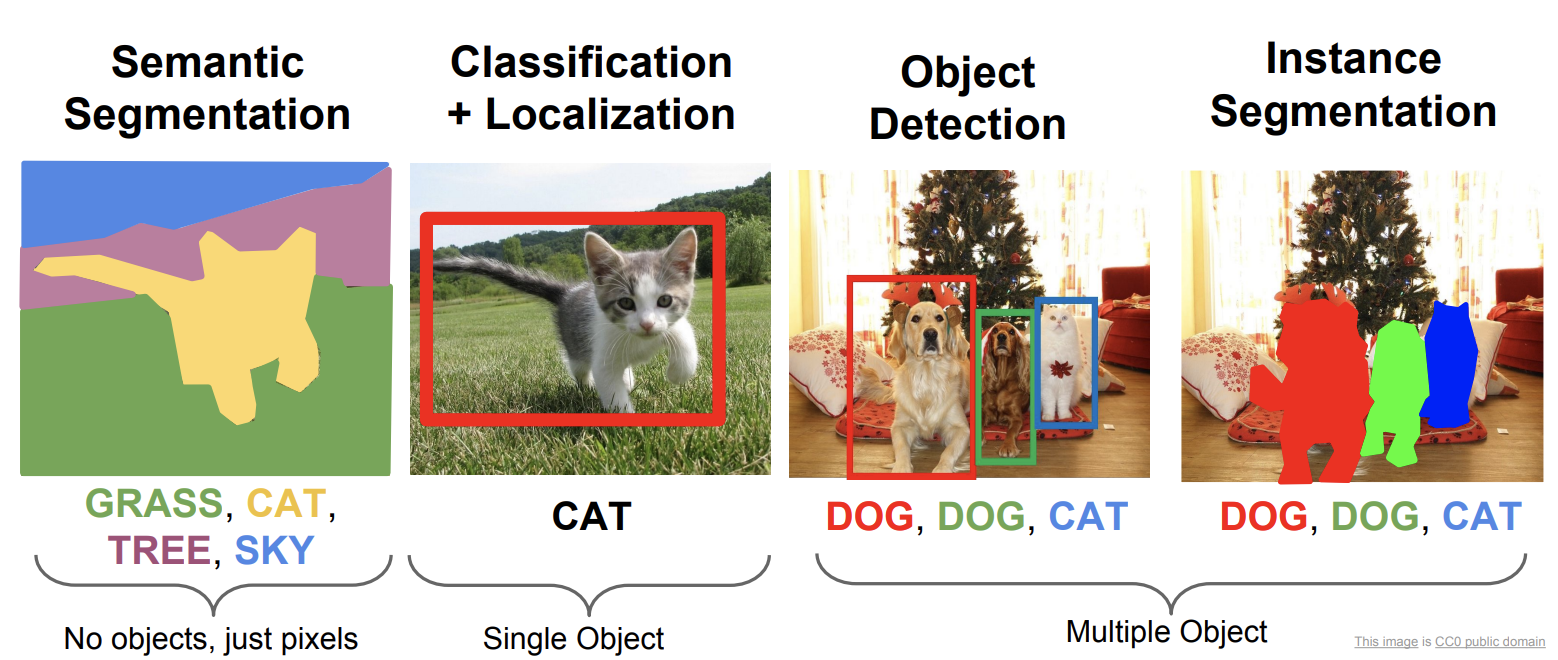
오늘은 Computer Vision Task 중에서 Semantic Segmentation Task의 성능지표에 대해 정리해봅시다. Segmentation Task는 Semantic Segmentation과 Instance Segmentation으로 나눌 수 있습니다. 최근에는 이 두 Task를 합친 Panoptic Segmentation라는 Task도 있습니다. Instance Segmentation과 Panoptic Segmentation은 다른 포스트에서 정리하도록 하겠습니다.
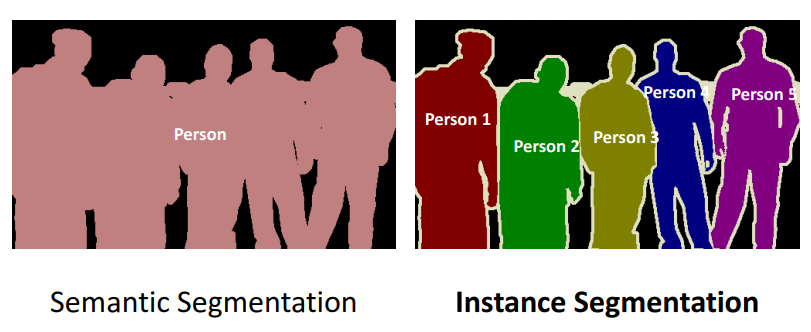
Semantic Segmentation은 Pixel-wise Classification으로 이미지에서 각 픽셀이 어느 클래스에 해당되는지 분류한 것입니다. 위의 그림과 같이 다른 Object라도 픽셀 단위에서 클래스를 구분하기 때문에 Object간의 구분은 하지 못합니다.
Instance Segmentation은 위의 그럼처럼 Semantic Segmentation하면서 각 Object까지 구분하여 분류한 것이라고 생각하면 됩니다.
Semantic Segmentation Metric
Semantic Segmentation에서는 모델 성능 비교를 위해 가장 보편적으로 사용하는 Benchmark metric으로는 Mean IoU가 있으며, 그 외에도 Pixel Accuracy와 Dice Coefficient가 있습니다. 각각에 대해 알아보도록 하겠습니다.
Pixel Accuracy
먼저 Pixel Accuracy는 말 그대로 픽셀 정확도입니다. 전체 픽셀 중에서 올바르게 분류된 픽셀의 비율로 표현되며 아래와 같이 나타낼 수 있습니다. \[Pixel Acc = \frac{TP+TN}{TP+TN+FP+FN}\]
아래와 같이 간단하게 구현할 수 있습니다.
![]()
IoU (Intersaction over Union)
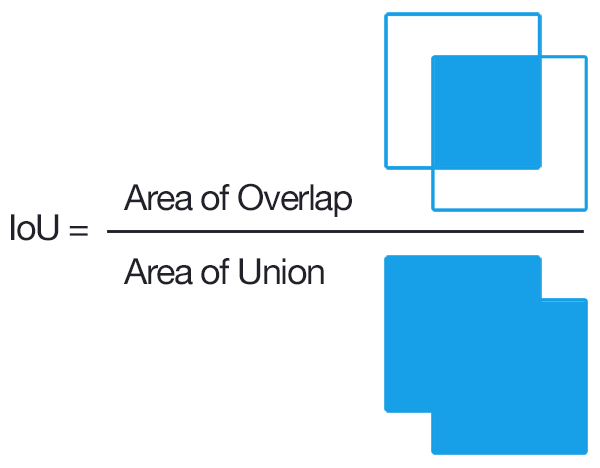
IoU는 Intersaction over Union의 약자로, 그 의미 그대로 합친 영역의 넓이(Union) 분의 겹치는 영역의 넓이(Intersaction) 비율을 의미합니다. Jaccard Index로 표현하기도 합니다. 코드 구현은 Mean IoU 파트에서 확인 가능합니다.
Mean IoU
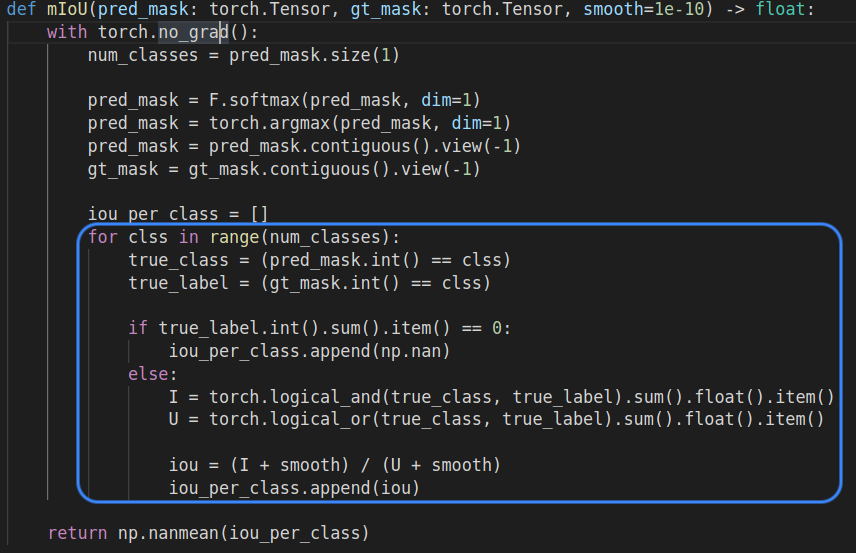
Semantic Segmentation에서 가장 흔히 사용되는 성능지표입니다. mIoU(Mean IoU)는 각 클래스별로 IoU를 계산하고 이들의 Mean으로 나타냅니다. 아래 식에서 \(C\)는 전체 클래스 개수이며, background를 포함하여 총 클래스 개수는 \(C+1\)이 됩니다. \[mIoU = \frac{1}{C+1}\sum_{c=0}^{C} IoU_c\]
파란색 Box부분이 각 클래스별 IoU를 구하는 부분이며 구한 값들의 mean값으로 mIoU를 구할 수 있습니다.
Dice Coefficient
Dice Coefficient는 Sørensen–Dice coefficient 또는 F1-Score로도 알려져있으며, 주로 Medical image Analysis에서 사용되는 metric입니다. \[Dice = \frac{2TP}{2TP+FP+FN} = \frac{2 \times {A}\cap{B}}{A+B}\]
Precision과 Recall의 조화평균인 F1-Score를 통분하여 정리하면 위의 Dice Coefficient 식처럼 정리가 됩니다. \[precision = \frac{TP}{TP+FP}\] \[recall = \frac{TP}{TP+FN}\]
\[f1\mbox{-}score = \frac{2 \times precision \times recall}{precision + recall}\] \[= \frac{2 \times \frac{TP}{TP+FP} \frac{TP}{TP+FN}}{\frac{TP}{TP+FP} + \frac{TP}{TP+FN}}\] \[= \frac{\frac{2 \times TP^2}{(TP+FP)(TP+FN)}}{\frac{TP(TP+FP+TP+FN)}{(TP+FP)(TP+FN)}}\] \[= \frac{2 \times TP}{2TP+FP+FN}\]
Reference
이 글이 도움이 되셨다면 추천 클릭을 부탁드립니다 :)

